Найдите периметр треугольника, если нанесена сетка из единичных квадратов.
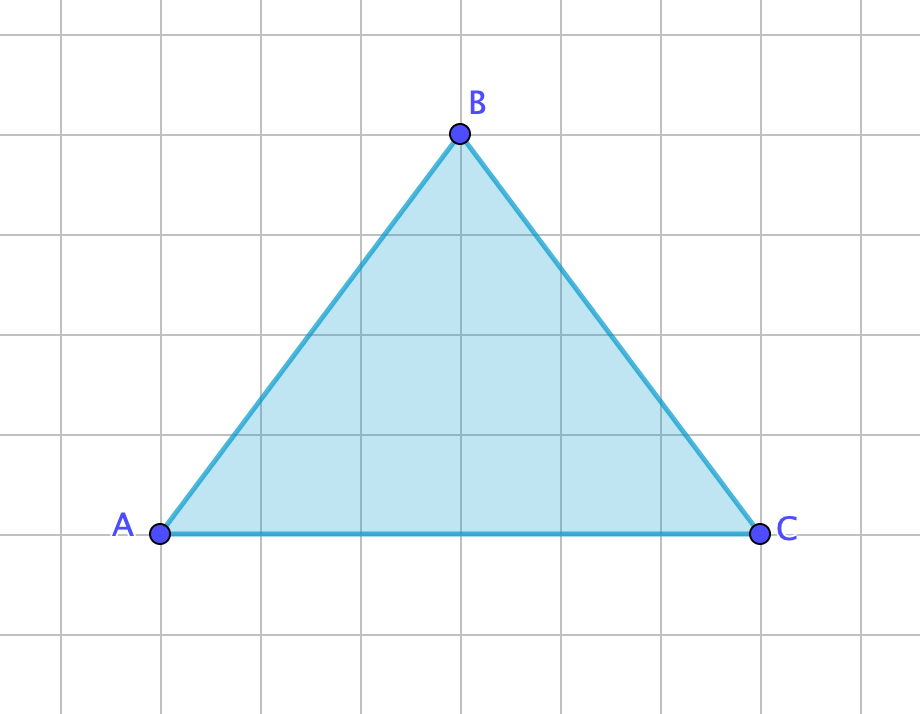
Проведем высоту к основанию \(\displaystyle AB{\small .}\) Получаем два прямоугольных треугольника \(\displaystyle ABD\) и \(\displaystyle BDC\) с катетами \(\displaystyle 3\) и \(\displaystyle 4{\small :}\)
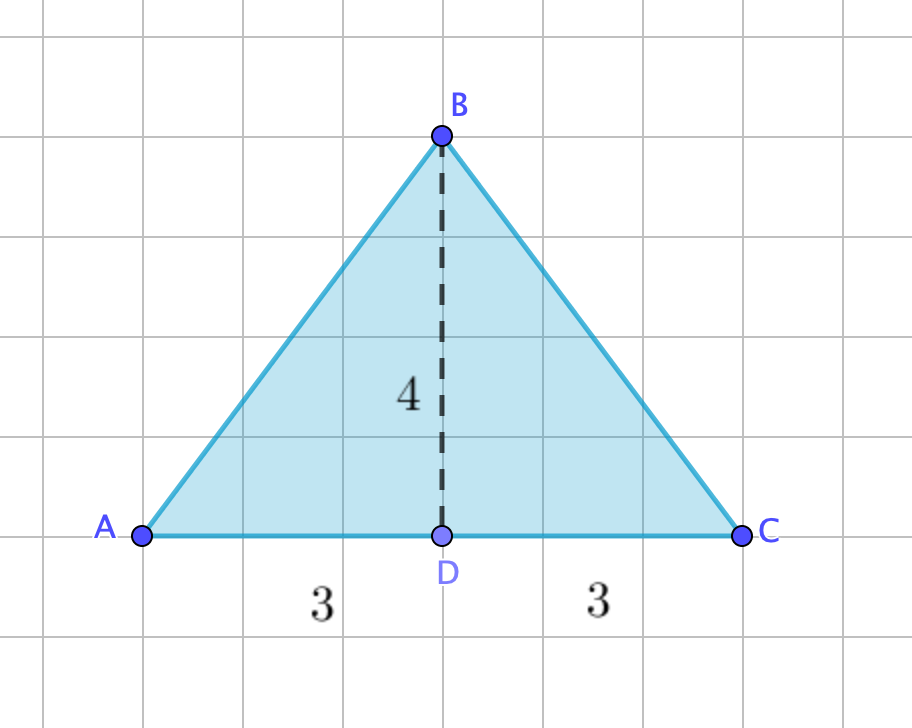
Тогда по теореме Пифагора гипотенузы \(\displaystyle AB\) и \(\displaystyle BC\) равны
\(\displaystyle AB=\sqrt{3^2+4^2}{ \small ,}\)
\(\displaystyle AB=\sqrt{25}{ \small ,}\)
\(\displaystyle AB=5\)
и
\(\displaystyle BС=\sqrt{3^2+4^2}{ \small ,}\)
\(\displaystyle BC=\sqrt{25}{ \small ,}\)
\(\displaystyle BC=5{\small .}\)
Таким образом, нам известны длины всех сторон треугольника:
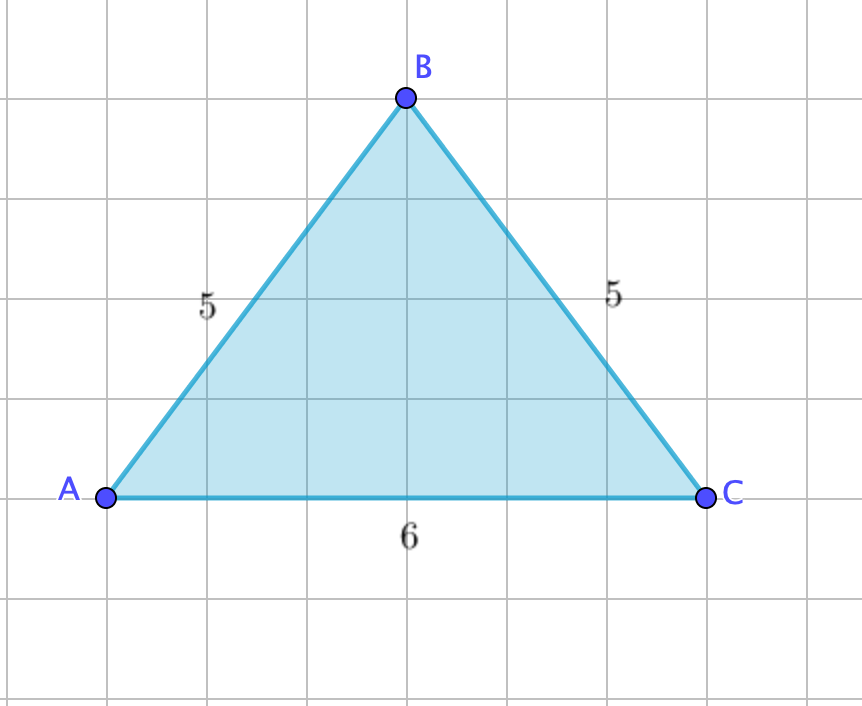
Периметр равен
\(\displaystyle AB+BC+CA=5+5+6=16{\small .}\)
Ответ: \(\displaystyle 16{\small .}\)