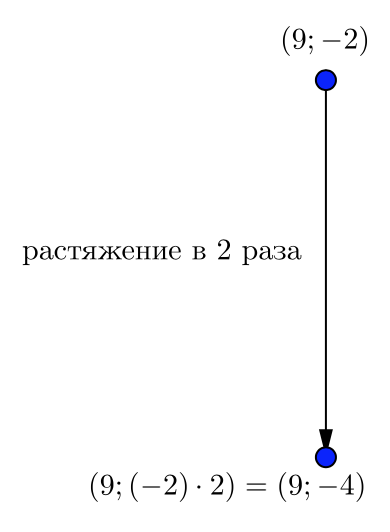
Найдите координаты точки, полученной растяжением точки \(\displaystyle (9;\, -2)\) вдоль оси \(\displaystyle \rm OY\) в \(\displaystyle 2\) раза.
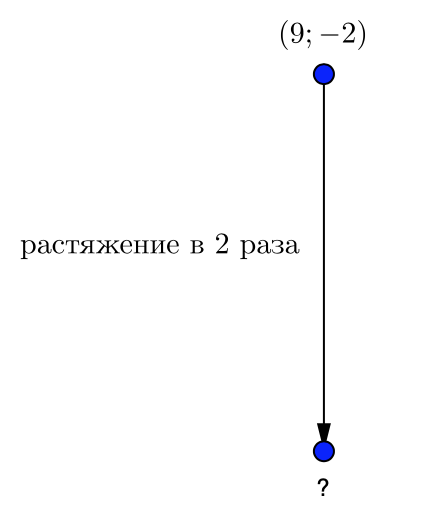
\(\displaystyle (9;\, -2) \rightarrow (\);\(\displaystyle )\)
Будем говорить, что точка \(\displaystyle (x_0;\, \color{red}{ k}\cdot y_0)\) получена растяжением вдоль оси \(\displaystyle \rm OY\) в \(\displaystyle \color{red}{ k}\) раз точки \(\displaystyle (x_0;\,y_0){ \small ,}\) если \(\displaystyle \color{red}{ k}>1{\small .}\)
Точка \(\displaystyle (x_0;\, \frac{y_0}{k})\) получена растяжением вдоль оси \(\displaystyle \rm OY\) в \(\displaystyle \frac{1}{k}\) раз точки \(\displaystyle (x_0;\,y_0){ \small ,}\) если \(\displaystyle 0<k<1{ \small ,}\)
так как \(\displaystyle (x_0;\, \frac{y_0}{k})=(x_0;\, \frac{1}{k}\cdot y_0)\) и \(\displaystyle \frac{1}{k}>1{\small .}\)
\(\displaystyle (9;\, -2){\small ,}\) после растяжения вдоль оси \(\displaystyle \rm OY\) вниз в \(\displaystyle 2\) раза, означает умножение координаты \(\displaystyle y\) (ординаты точки) на \(\displaystyle 2{\small .}\)
Поэтому